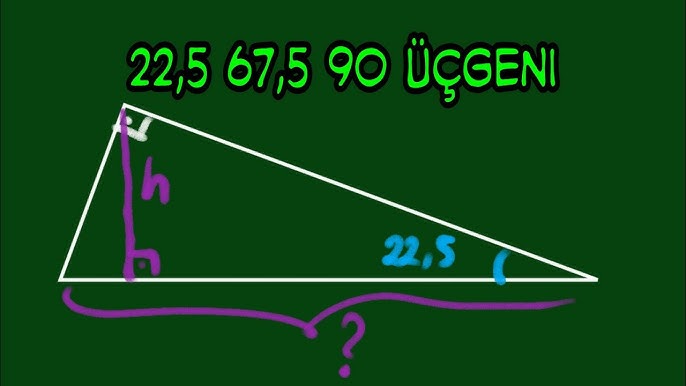
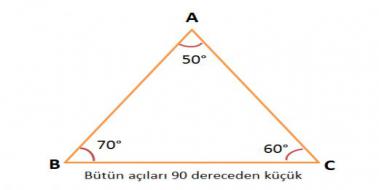
Quote Orijinalden alıntı brknzbz üçgeninde şu bağıntılar vardır 1 (kök31)k (kök31)k (2kök2)k sırasıyla derecelerin karşılarındaki kenarların aralarındaki bağıntıdır bu 2 15 derecenin hemen yanına doğru bir doğru parçası indirerek ikizkenar üçgen oluşturup (1515 derece şeklinde) küçük bir 0 ve üçgeni oluşturmaküç kenarının uzuluğuda birbirinin birebir aynısı olan üçgenlere denir Eşkenar üçgende iç açılarının dereceleri de birbirine eşittir ve herbir açının değeri 60 derece olur Eşkenar Üçgenin Çevresinin Uzunluğu;Sin Cos Tan Cot 4590 değerleri kaçtır ?
45 45 90 Ucgeni Matematikce
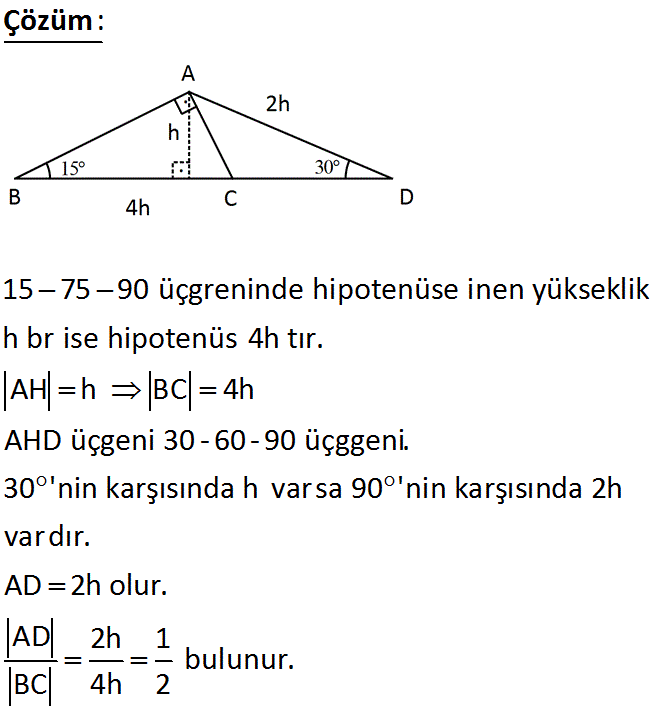
15 75 90 üçgeni alan formülü
15 75 90 üçgeni alan formülü-Refleks 4 15°– 75°– 90° Üçgeni 645;90 15 75 ucgeninin ozelligi # tl bina, daire aksaray tl peŞİnatla faİzsİz kredİsİz ev sahİbİ olun paŞacik mahallesİnde tl 31 daİreler gelİn temelden satiŞ yapalim tl ye sİzİn olsun 31 Hayat Eve Sığar uygulamasının yeni özelliği 'Güvenli Alan' ile AVM, restoran, kafe ve taksilerin koronavirüs açısından güvenli olup olmadığı anlık olarak takip edilebilecek




Ucgenin Alani Ortaokul Matematik
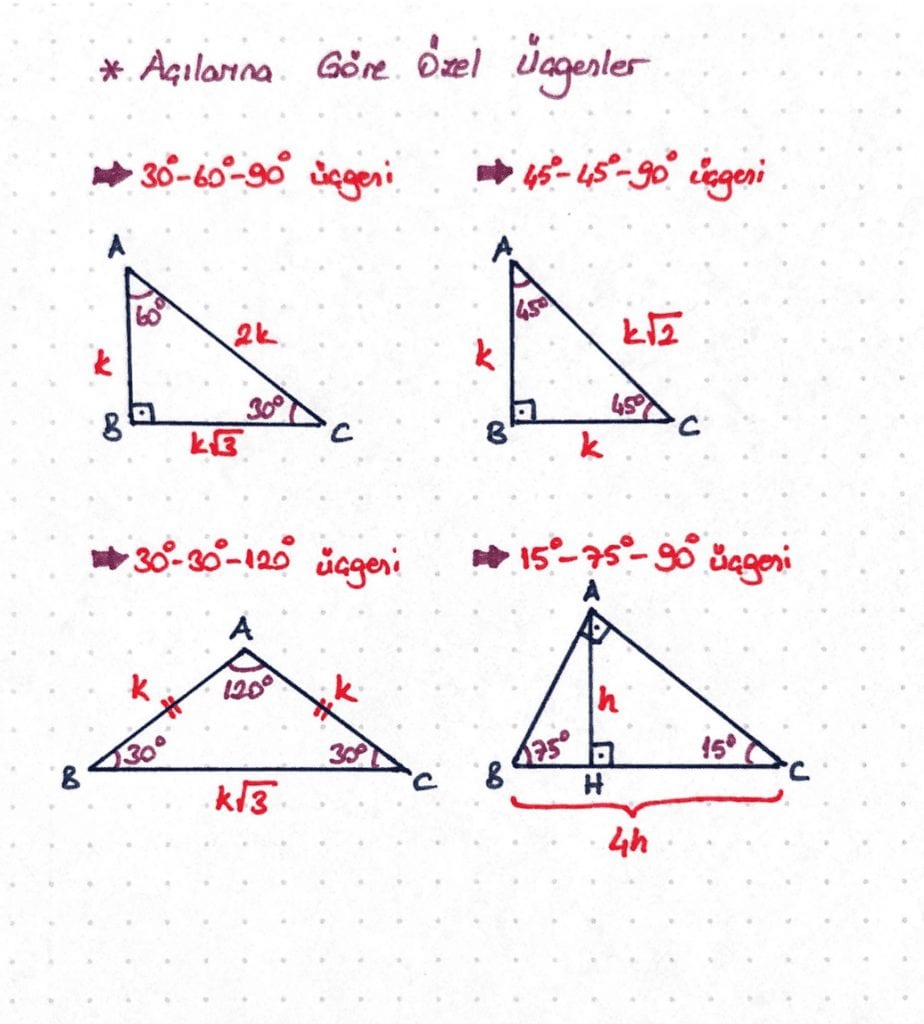
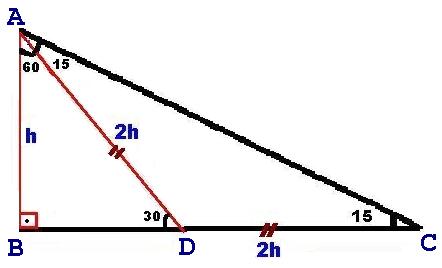
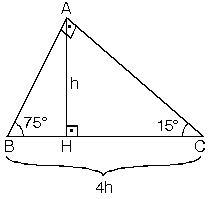
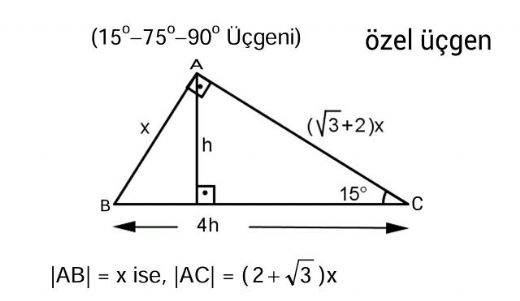
Eğlenceli görsellerle dik üçgen ÜYELİK GİRİŞİ Kullanıcı adı15 75 90 üçgeninde hipotenüse indirilen yükseklik hipotenüsün dörttebiridir kuralının ispatını bu videoda bulabilirsiniz özel bir dik üçgendir 90 derecelik açının karşısında hipotenüs bunulunur Bu 90 derecelik açının olduğu yerden hipotenüse indirilecek dik (yani yükseklik) h olursa hipotenüs de 4h olacaktır 5 ayrıca 75 ten uzatılacak kol ile 15 15 eş üçgeni ve 30 60 90 dik üçgeni
Refleks 5 22,5°– 67,5°– 90° Üçgeni 549;Dik üçgenin çevresi formülü Çevre = ( a b h) b= dik açının birinci komşu kenarı c= dik açının ikinci komşu kenarı h= hipotenüs Bunu bir örnek vererek açıklayalım;D) 15 3 E) 15 5 ÇÖZÜM 2u = 7 8 9 = 24 birim ise, u = 12 olur Buna göre, A(ABC) 12 (12 7) (12 8) (12 9) 12 5 4 3 12 5 br2 bulunur Cevap C'dir 3 Üçgenin Trigonometrik Alan Formülü Bir üçgenin alanı, iki kenarının uzunluğu ile bu kenarlar arasındaki açının
15 75 90 ÜÇGENİ ÖZELLİKLERİ 15 75 90 üçgeni bir dik üçgendir İç açıları toplamı 180 derecedir Dış açıları toplamı 360 derecedir İki dar açısının toplamı diğer 7 Sınıf Çokgenler, Doğrusal olmayan 3 veya daha fazla noktanın aynı düzlemde art arda doğru parçaları ile birleşiminden oluşan kapalı geometrik şekillere çokgen denir Çokgenlerin Köşegenleri, Çokgenlerin karşılıklı kenarlarının iki ucu komşu köşelerdir Çokgenin komşu olmayan iki köşesini birleştiren doğru parçalarına çokgenin köşegenleri denir 15 75 90 Üçgeninde Dikme Özelliği 15 75 90 üçgeni ile ilgili bilmemiz gereken ve çok basit olan bir dikme özelliği vardır 15 75 90 üçgeni içerisinde 90 dereceden hipotenüse indirilen bir dikmenin uzunluğu hipotenüsün 4'te biri kadar olur Yani dikme ile hipotenüs arasında h




Southern California Engagement Photographer Ventura Beach Ventura California Stephanieflores Com Blog




15 75 90 Ucgeni Not Bu
Üçgende Sinüslü Alan Formülü İSPAT onurcalis, 03 Eyl 14 0133 (0 msj) Üçgeni (2√3) İSPAT onurcalis, 02 Eyl 14 1448 (0 msj) mukemmel dikdortgen Serkan, 12 Ara 13 0049 (1 msj) rasyonel dörtgen gereksizyorumcu, 11 Ara 13 30 (1 msj) Dairede Alan (İSPAT) Serkan, 12 Ağu 13 19 (1 msj) Üçgeni Kenar Bağıntısı ( İSPAT ) tenten1,Refleks 5 22,5°– 67,5°– 90° Üçgeni 549;Dik Üçgenin Alan Hesaplama Formülü Nedir?




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz
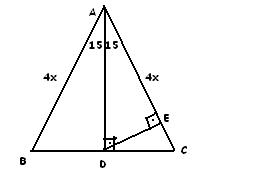



15 75 90 Ucgeni Kenar Bagintisi Ispat
S eşkenar üçgen, üçgende alan, üçgenler Ilgili YAZILAR Silindirin Hacmi Yorum yapılmamış Şub 17, 19 15 75 90 Üçgeni Yorum yapılmamış Şub 5, 19 Altıgenin En Uzun Köşegeni Yorum yapılmamış Tem 21, Sekizgenin Özellikleri Yorum yapılmamış Eyl 28, 19 Yazar Eşkenar Üçgen Alan Formülü;Örnek Bir dik üçgende dik açının komşu kenarlarının uzunlukları sırasıyla 6 cm, 8
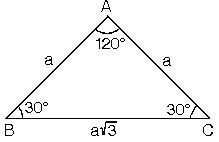



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




3 4 5 Ucgeni Ve Ozellikleri Not Bu
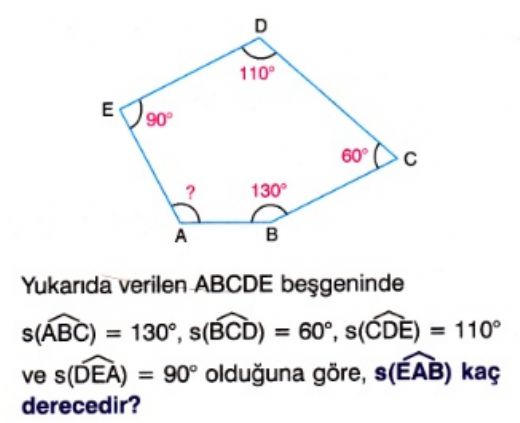
5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC =Birim Fonksiyon Nedir ? A) 8 B) 9 C) 10 D) 12 E) 16 30 Dörtgenin iç açıları toplamı 360 dir 2x 2y 160 140 360 olmalıdır 2 x y 300 360 2 x y 60 x y 30 dir AKD üçgenin iç açıları toplamından;




List Of Trigonometric Identities Wikipedia




15 75 90 Ucgeni Akilli Geometri
15 75 90 üçgeninin kenarları arasındaki bağıntının nerden geldiğinin ispatını bu videoda izleyebilirsiniz12 A B C E 75 15 H 15 x EH = x uzunluğudur Buradan AB = 4 EH olduğundan, 12 = 4 x x = 3 br bulunur Cevap A'dır (vii)(30 30 1 ) ÜÇGENİ A B C 30 30 1 x x x 3 Bu üçgende, 1 nin karşısındaki kenar, eş kenarlardan birinin 3 katına eşittir AB = AC15 75 90 üçgeni özelliklerinin ispatı Üçgende çevreye bağlı alan formülünün ispatı Üçgende sinüslü alan formülünün ispatı Fonksiyonlarda ters alma işleminin bileşke üzerine dağılmasının ispatı İki nokta arası uzaklık formülünün ispatı Düzlemde doğru parçasının orta noktası formülünün ispatı




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt



Dik Ucgenin Alani Nasil Bulunur Dik Ucgenin Alan Hesaplama Formulu Nedir Egitim Haberleri
üçgeni kenarları arasındaki oran ekşi up Üçgeni (2√3) İSPAT 15 75 90 Üçgeni Not Bu triangle Math, Trigonometry, Right Triangles ShowMe Finding the area of a $$ triangle with the length of What are the side relationships of a triangle? Trigonometrik olarak ise üçgeni özelliklerinden yararlanarak yüksekliğin olduğu ortaya çıkmaktadır Üçgenlerde alan hesaplama yolu taban uzunluğu ile yüksekliğinRefleks 6 Küçük Üçgenden Yola Çıkarak Büyük Üçgeni Refleks 19 Sinüs Alan Formülü Yardımı İle İki Üçgenin Alanları Oranını Bulma 941;
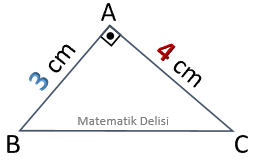



2 Kok 5 3 Ucgeni




Geometry Formulas
Hipotenüs 90 derecelik açının karşısındaki en uzun kenardır Eşkenar üçgenin alanı;15 75 90 Ucgeninin Ozellikleri Nelerdir Ucgen Gen Tr Dik Ucgen 17 22 5 67 5 90 Ucgeni Matematik 15 75 90 Ucgen Ozelligi Ve 5 Ornek Cozum Youtube Effective Dose Versus Patient Thickness Ap For Ct Urography Ctu Ozellik 5 Bilgicik Com The 18 72 90 And 36 54 90 Triangles Robertlovespi Net Health, general Obsessive compulsive disorder Beliefs, opinions and attitudes 15 75 90 Üçgeni Özellikleri 15 75 90 Üçgeninde Kenarların Oranı 15 75 90 üçgeninde kenarlar arasında belirli bir oran bulunması zorunluluğu vardır Bu oran formül ezberlendiği zaman rahat bir şekilde ortaya çıkartılabilir Eğer formülü ezberlemezseniz farklı yöntemlerle bu hesaplamaları yapabilirsiniz Fakat oldukça yoğun bir zaman ayırmanız gerekiyor




15 75 90 Ucgeni




Dik Ucgen 5 45 45 90 Ucgeni Geometri Metin Hocam Youtube
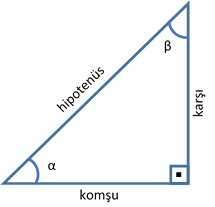
1 Düzine Kaç Adettir ?Refleks 4 15°– 75°– 90° Üçgeni 645;Özel Üçgenler DİK ÜÇGEN Bir açısının ölçüsü 90° olan üçgene dik üçgen denir Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir Hipotenüs üçgenin daima en uzun kenarıdırşekilde, m(A) = 90° BC kenarı hipotenüs AB ve AC kenarları dik kenarlardır PİSAGOR BAĞINTISI Dik üçgende dik kenarların uzunluklarının



15 75 90 Ucgeni




Ispat 15 75 90 Ucgeni Tyt Geometri Ozel Ucgenler Youtube
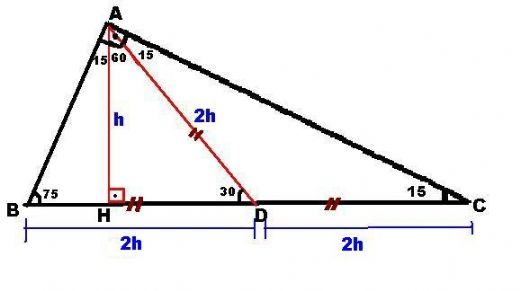
M(AKD) x y 180 m(AKD) 150 dir Sinüs alan formülünden A(AKD) bu 01Şub lunabilir 1 1 1 32 A(AKD) 4 8 sin150 32 8 buluruz 2 2 2 4 Sinüs alan formülü bilinmiyorsa, bir üçgen çizip hesaplama yapmak 15 75 90 üçgeni özellikleri çoğu zaman dik bir üçgene dikme indirildiğinde ortaya çıkar Görselden de gördüğünüz gibi dik üçgenin, dik açısından tabana doğru bir dikme indirilmiş Daha sonra karşımıza iki adet 15 75 90 üçgeni çıkmış Yukarıdaki 15 75 90 üçgeni özellikleri, bu üçgenlerde kullanılarak sorunun doğru yanıtı bulunur15 75 90 üçgeni özelliği 15 75 90 üçgeni özel bir dik üçgendiryükseklik değerine x dersek hipotenüs 4x tir Sitemizde yer alan dosya ve içeriklerin telif hakları dosya ve içerik gönderenlerin kendilerine veya yetki verdikleri kişilere aittir 15 75 90 üçgeni üçgenler geometrinin temelini oluşturmaktadırdüzlemde 15 75 90 üçgeni özelliklerinin ispatını gösteriyoruz



15 75 90 Ucgeni Kurali Nedir 15 75 90 Ozel Ucgeni Ozellikleri Ve Ornek Sorular Limkhub




15 75 90 Ucgeni
Top 15 75 90 Alan Pictures Harry Kane's 100 Premier League goals for Tottenham theSabit Fonksiyon Nedir ? Öyleyse kenar uzunluğu a birim olan bir düzgün altıgenin alan formülü nedir?



45 45 90 Ucgeni Matematikce




15 75 90 Ucgeni Ozellikleri Ve Kurali Ogrenci Yardim
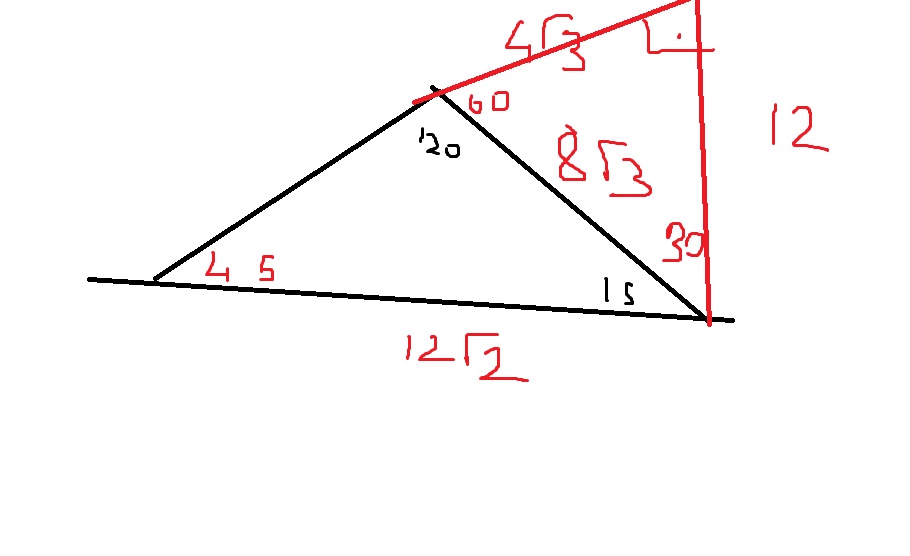
Eşkenar üçgen gibi özel üçgenlerde yukarıda verilen genel üçgende alan formülü yerine bazı özel formüller kullanırız Bunun sebebi eşkenar üçgenin üç kenar uzunluğu eşit olduğu için, bu üç kenara ait yüksekliklerin uzunluğunun da eşit olmasıdır Aynı zamanda kenarRefleks Sinüs Alan Formülü Buradan A(ABC)= 125s/9 O zaman istenen oran 18/125 olur C3) A dan DC ye bir yükseklik çizip açılar bulunduğunda yüksekliğin hemen solunda 45,4590 üçgeni bulunur hipoteüs 4 dür Buradan dik kenarlar 2√ 2 olur Yani büyük dik üçgenin yüksekliği 2√ 2 dir Büyük üçgen 15,75,90 üçgeni olduğundan yükselik a ise hipotenüs 4a dır özelliğinden BC=8√ 2 dir



15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz



Populer Icerik
15 75 90 üçgeni özel kuralları yukarıda verildiği şekildedir Açılarını bilinmesiyle çok rahat uzunlukları da bilinmektedir Açıları ve uzunluk ölçüleri bilinen üçgenlerin alan hesaplama işlemi de oldukça basittir Yani bilinen 15 75 90 üçgeni kuralı ile o özel üçgenle ilgili açı, uzunluk, yükseklik ve alan gibi sorulan bütün soruları bilmek mümkündür Ya da sin1 = √3 / 2 formülü size yardımcı olabilecek farklı bir yöntem Eğer bu yöntemler aklınıza gelmezse bu durumda tepe açısından bir dikme indirmeniz işinizi kolaylaştıracaktır Bu sayede iki adet eş 30 60 90 üçgeni oluşturursunuz ki bunun bütün özelliklerinden yararlanabilirsiniz90 75 15 Üçgeni, 90 75 15 Üçgeni Özellikleri ucgengentr üçgeni 15 45 1 özel üçgeni var mı?varsa kuralı nedir Eodevcom




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz




Geometry Formulas
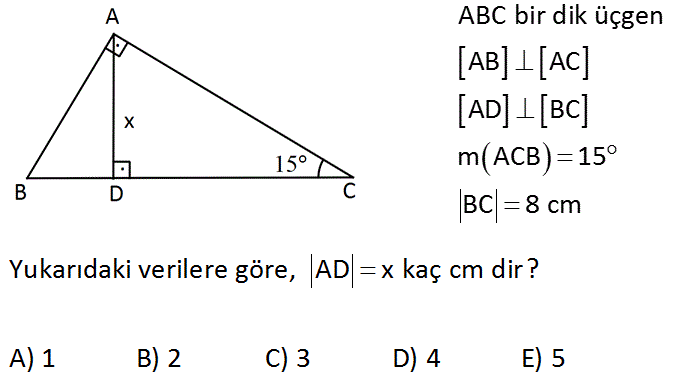
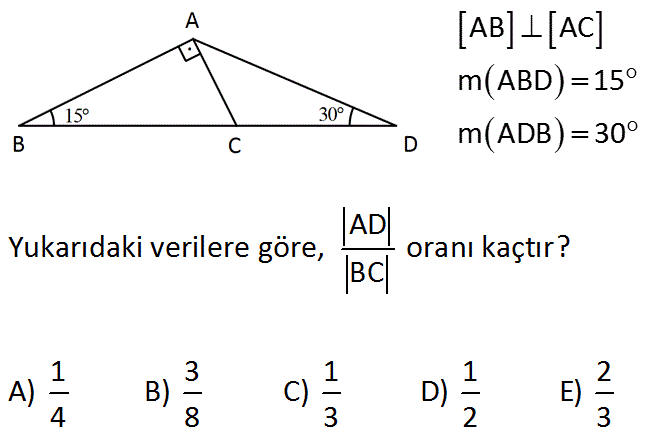
AD C üçgeni 15 75 90 üçgenidir 15 75 90 üçgeninde hipotenüse inen yükseklik, hipotenüsün 4' te 1'i dir 4 2 x 2 cm bulunur 4 12 ABC eşkenar üçgen, AB // AD AE AD ED 2 cm Yukarıdaki verilere göre, BE x kaç cm dir?DİK VE ÖZEL ÜÇGENLER TEST1 TYTAYT Geometri konuları dik ve özel üçgenler test1 ve çözümleri Geometri konuları dik üçgenler, özel üçgenler, 30 60 90 üçgeni, 45 45 90 üçgeni, 15 75 90 üçgeni, 15 30 135 üçgeni, öklid, pisagor, muhteşem üçlü, kenarlarına veIkizkenar 15 75 90 Ucgeni Yardim Edebilir Misiniz Cozemedigim 75 15 90 özel üçgeni bu özel üçgende 15 derecelik açının karşısında yer alan kenar uzunluğu 1cm alınırsa 75 derecelik açının karşısındaki kenarın uzunluğu 2 3 cm olur şekildeki gibi iki üçgene ayırırsak 15 15 150 ve 30 60 90 labla ise lbdla3 olacaktır ve




15 75 90 Ucgeni Ozellikleri Ve Kurallari




Ucgende Alan Formulleri Ve Bagintilari Matematik Ogretmenleri
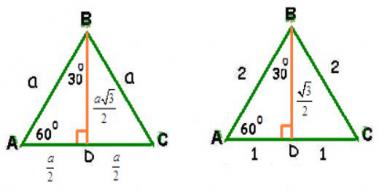
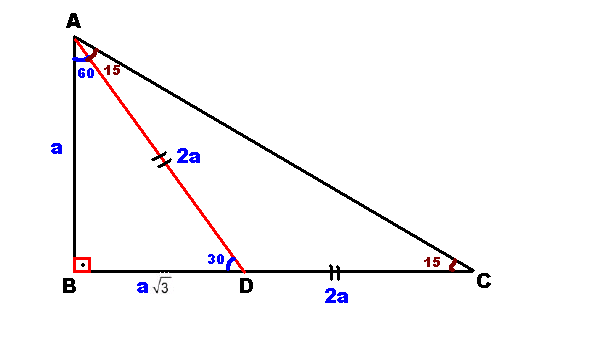
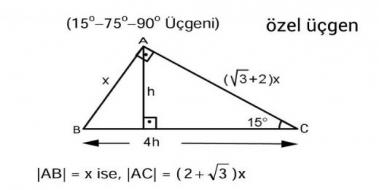
üçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar 2 3 {\displaystyle 2 {\sqrt {3}}} cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir Ayrıca bu üçgende hipotenüse indirilen dikme 15 ve 60 olarak böldüğünüzde ise karşınıza bir 30 60 90 üçgeni ve de diğer tarafta kalan açıları 15 15 150 olan bir ikizkenar üçgen çıkacaktır bu durumda şöyle bir sonuç çıkar karşımıza 15 derecenin karşısındaki kenara a değerini verirsek, 75 derecenin karşısındaki kenar da 2aakök3 olacaktır 90'nın karşını da pisagor teoreminden hesaplayın, işinizMuhteşem Üçlünün İspatı Üçgende Sinüslü Alan Formülü İSPAT 22,5 67,5 90 Üçgeni (1√2) İSPAT Üçgeni (h4h) İSPAT Üçgeni (2√3) İSPAT mukemmel dikdortgen rasyonel dörtgen Dairede Alan (İSPAT) Üçgeni Kenar Bağıntısı ( İSPAT )




Sozel Geometri Sorulari Pdf Ucretsiz Indirin



15 75 90 Ucgeni Ozellikleri
Eşkenar üçgen gibi özel üçgenlerde yukarıda verilen genel üçgende alan formülü yerine bazı özel formüller kullanırız Bunun sebebi eşkenar üçgenin üç kenar uzunluğu eşit olduğu için, bu üç kenara ait yüksekliklerin uzunluğunun da eşit olmasıdır Aynı zamanda kenarüçgende alan soruları( 4 tane ) Sıcak Fırsatlarda Tıklananlar Editörün Seçtiği FırsatlarQuora Angle Sums and the Right Triangle – GeoGebra Math off the grid




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz




15 75 90 Ucgeni Pow Bylge
Ne olur Cevap Yazın » Ruşen Aydın 1526 Hipotenüs Uzunluğu 108,1666 birim Komşu Kenar Uzunluğu 90 birim Karşı Kenar Uzunluğu 60,0001 birimRefleks 6 Küçük Üçgenden Yola Çıkarak Büyük Üçgeni Refleks 19 Sinüs Alan Formülü Yardımı İle İki Üçgenin Alanları Oranını Bulma 941;Bir Düzine Kaç Tanedir ?



1




Ucgende Alan Formulleri Ve Bagintilari Matematik Ogretmenleri
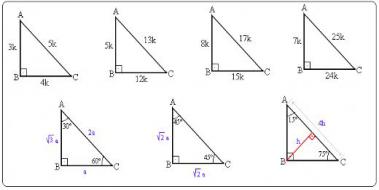
Dun ozel okul sinavinda sorulan şu soruyu cozemedim lutfen yardim edermisnizuc kenar uzunlugu bilinemeyen ama cevresi 75 olan dik ucgenin ac_bkare=?Read özel üçgenler (15°75°90° üçgeni) from the story Matematik Formülleri by TheMuhammedALI with 1,850 reads geometri, analatikgeometri, matematik Resime b 15 75 90 Üçgeni (15°, 75°, 90°) dik üçgeninde hipotenüsü ait yükseklik hipotenüsün dörtte birine eşittir 30 30 1 Üçgeni 30 – 30 – 1 ikizkenar üçgeni iki adet 30 – 60 – 90 dik üçgeninden oluşur 1 0 'nin karşısındaki kenar ikiz kenarların √3 katına eşittir Dik Üçgen ve Öklid Kuralları Dik üçgenlerde 90°'lik açının bulunduğu




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ozel Ucgeni Ozellikleri Ve Ornek Sorular Egitim Haberleri




Ucgenin Alani Nasil Bulunur Ucgen Alan Formulleri Ve Cesitleri Bilgeniz Com
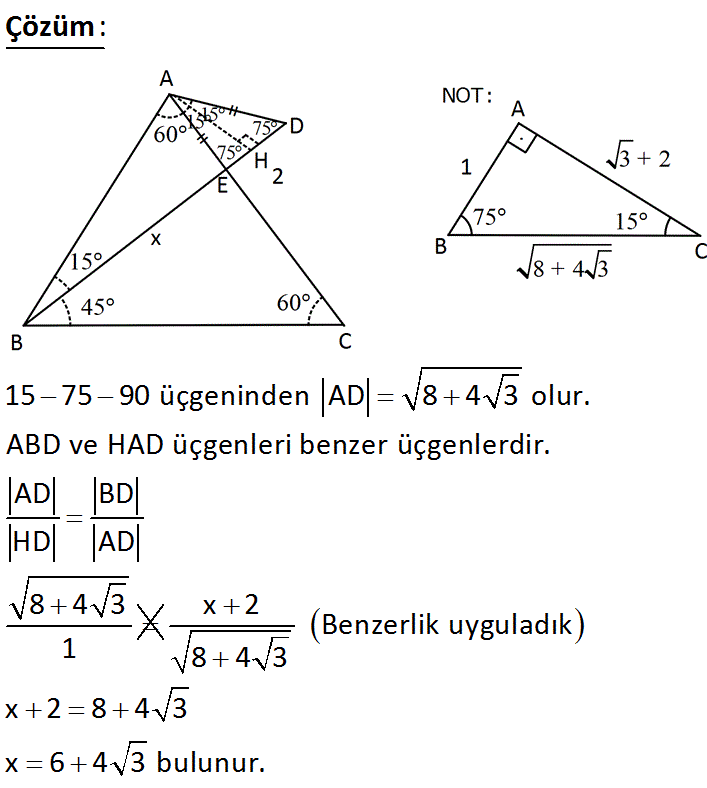
いろいろ 15 75 90 üçgeni alan bulma 75 90 üçgeni alan bulma Thanh Ngọc 7月 16, 21 Altıgen alan formülü alanını 75 cm 2 bulduysanız ve eksik üçgenin alanını ise 続きを読む 最も欲しかった 4年生 理科 月の動き プリント 年生 理科 月の動き プリント Thanh Ngọc 7月 15, 21 新興出版社 ×A) 2 3 4 B) 2 3 6 C) 4 3 2 D) 4 3 4 E) 4 3 6 wwwmatematikkolaynet Çözüm 15 75 90 üçgeninden AD 8 4 3 olur ABD ve HAD üçgenleri benzer üçgenlerdir2 Basamaklı En Büyük – Küçük Doğal Sayı Kaçtır ?




15 75 90 Ucgen Ozelligi Ve 5 Ornek Cozum Youtube




Dik Ucgen 17 22 5 67 5 90 Ucgeni Evde Egitim Matematik Ders Calisma Ipuclari
Hipotenüs 90 derecelik açının karşısındaki en uzun kenardır Eşkenar üçgenin alanı; 5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC =Refleks Sinüs Alan Formülü




15 75 90 Ozel Ucgeni Ozellikleri



30 30 1 Ucgeni Kenar Iliskisi Ve Alan Formulu Ispati Youtube
Özel üçgenlerden bilinmesi gereken üçgenlerden bir tanesi de 15 75 90 üçgenidir Bu üçgenin bilinmesi soruların çözülmesi açısından basitlık sağlamaktadır 15 75 90 üçgeni bir dik üçgendir Her üçgende olduğu gibi iç açıları toplamı 180, dış açıları toplamı ise 360 derecedir Bu dik üçgende kenar uzunlukları için Pisagor teoremi uygulanmaktadır 15 75ABE üçgeni (15 75 90 ) üçgenidir ABE üçgeninde E nin AB ye en yakın uzaklığı hipote nüse ait yükseklik;Ardışık Sayıların Tüm Formülleri;



15 75 90 Ucgeni



15 75 90 Ucgeni Ozellikleri
Sin Cos Tan Cot değerleri kaçtır ?




Dik Ucgen 16 15 75 90 Ucgeni Temel Matematik Matematik Felsefesi Evde Egitim




Matnℓsnye On Instagram Buyuk Hazine Serisine Bu Guzel Postla Guzel Bir Ara Tum Onemli Geometri Formuller Bir Arada Like Save Geometri Matematik Kalkulus



最新 75 15 90 Ucgeni シモネタ



45 45 90 Ucgeni Matematikce




Kisa Yollar 2 15 75 22 5 67 5 Derecenin Trigonometrik Degerleri Youtube




15 75 90 Ucgeni Ozellikleri Ve Kurali Ogrenci Yardim




Ucgenin Alani Nasil Bulunur Ucgen Alan Formulleri Ve Cesitleri Bilgeniz Com




15 75 90 Ucgeni




30 60 90 Ucgeni Ve Ozellikleri Not Bu
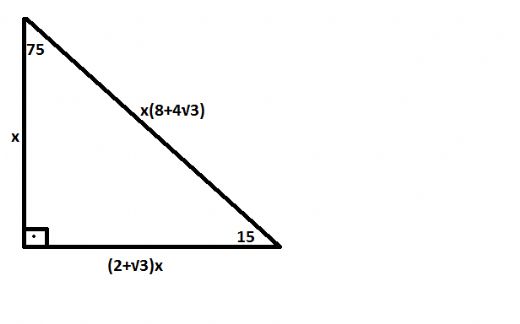



15 75 90 Ucgeninin Ozellikleri Nelerdir




15 75 90 Ucgeni Ozellikleri Ve Kurali Soru List



15 75 90 Ucgeni Webders Net




We Re Still Here Crooked Lane Farm Folk School



15 75 90 Ucgeni Ozellikleri



Journals Tubitak Gov Tr Earth Issues Yer 29 7 Yer 29 7 5 06 11 Pdf



1




Ucgende Alan Formulleri Ve Bagintilari Matematik Ogretmenleri




15 75 90 Ucgeni Pow Bylge



Ucgen Ve Cokgenlerle Ilgili Soru Ve Alistirmalar




Matematik Formullerinin Teoremlerinin Ispatlari Ozeldersci
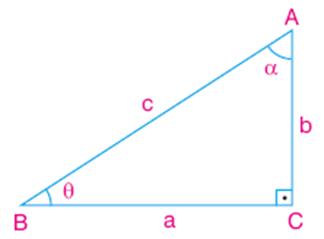



Dik Ucgende Trigonometrik Oranlar




15 75 90 Ucgeni




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt



1



15 75 90 Ucgeni



Q Tbn And9gcto4bnkzt2y Mlslzezgmlwske7ayni5axjtwi4doy0xjos1y Usqp Cau



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




15 75 90 Ucgeninin Ozelligi Nedir Eodev Com




15 75 90 Ozel Ucgeni Oluyor Ama Ben Sadece O Ucgenin Yukseklik Le Ilgili Ozelligini Biliyorum Baska Eodev Com




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz




15 75 90 Ucgeni Ozellikleri Ve Kurali Ogrenci Yardim



Dik Ucgen Ve Ozellikleri 21 Kpss Guncel Bilgiler



Ucgen Ve Cokgenlerle Ilgili Soru Ve Alistirmalar




Dik Ucgen Wikiwand



15 75 90 Ucgeni



Lrhe3ie6ibz Ym



15 75 90 Ucgeni Ozellikleri



15 75 90 Ucgeni 2 3 Ispat




Ucgenin Alani Nasil Bulunur Ucgen Alan Formulleri Ve Cesitleri Bilgeniz Com



Files Eric Ed Gov Fulltext Ej Pdf



90 75 15 Ucgeni Ozellikleri




Ucgenin Alani Ortaokul Matematik



15 75 90 Ucgeni




15 75 90 Ucgeni Webders Net




En Hizli 30 60 90 Ucgeni Trigonometrik Oranlari Sorulari



Dik Ucgende Trigonometrik Hesaplamalar



Dik Ucgen Vikipedi




Ucgenin Alani Nasil Bulunur Ucgen Alan Formulleri Ve Cesitleri Bilgeniz Com



Populer Icerik




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ozel Ucgeni Ozellikleri Ve Ornek Sorular Limkhub




Umut Matematik Kurs Merkezi Home Facebook



Alonot Com Wp Content Uploads 21 01 Tu Cc m Geometri Formu Cc lleri Pdf




15 75 90 Ozel Ucgeninin Kenar Bagintilari Nedir Eodev Com




Matematik Formulleri Ozel Ucgenler 15 75 90 Ucgeni Wattpad
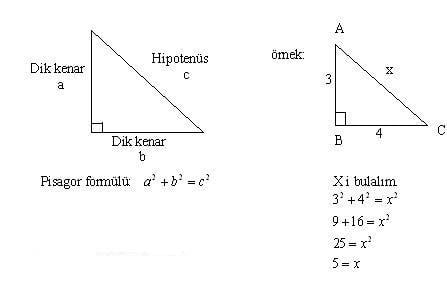



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




15 75 90 Ucgeni Eodev Com




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ucgeni Ozellikleri Ve Sorulari
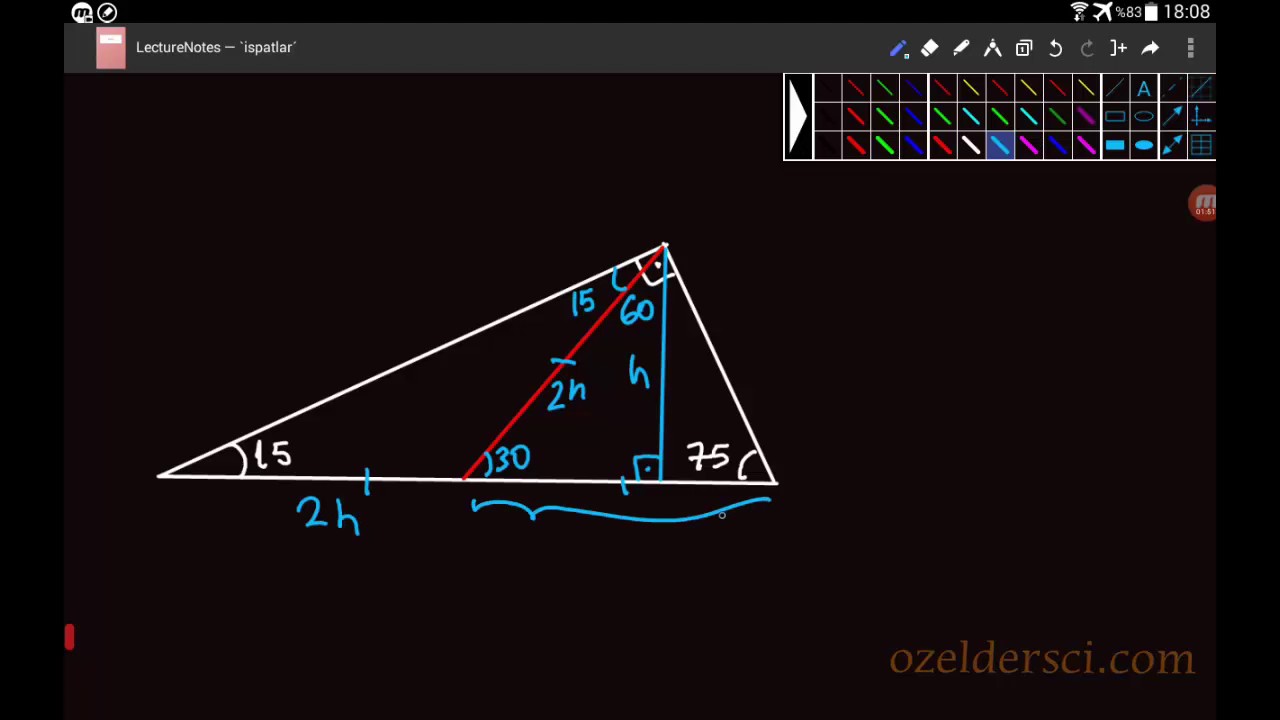



15 75 90 Ucgeni Ozelliklerinin Ispati Youtube




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt
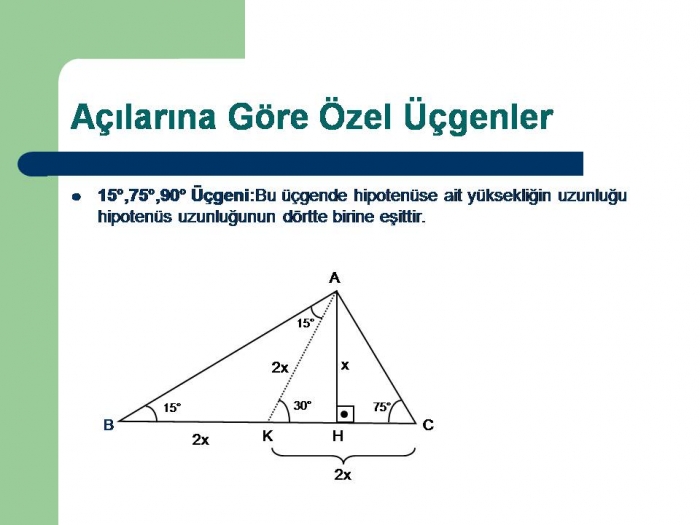



15 75 90 Ucgeni Uludag Sozluk




15 75 90 Ucgeni
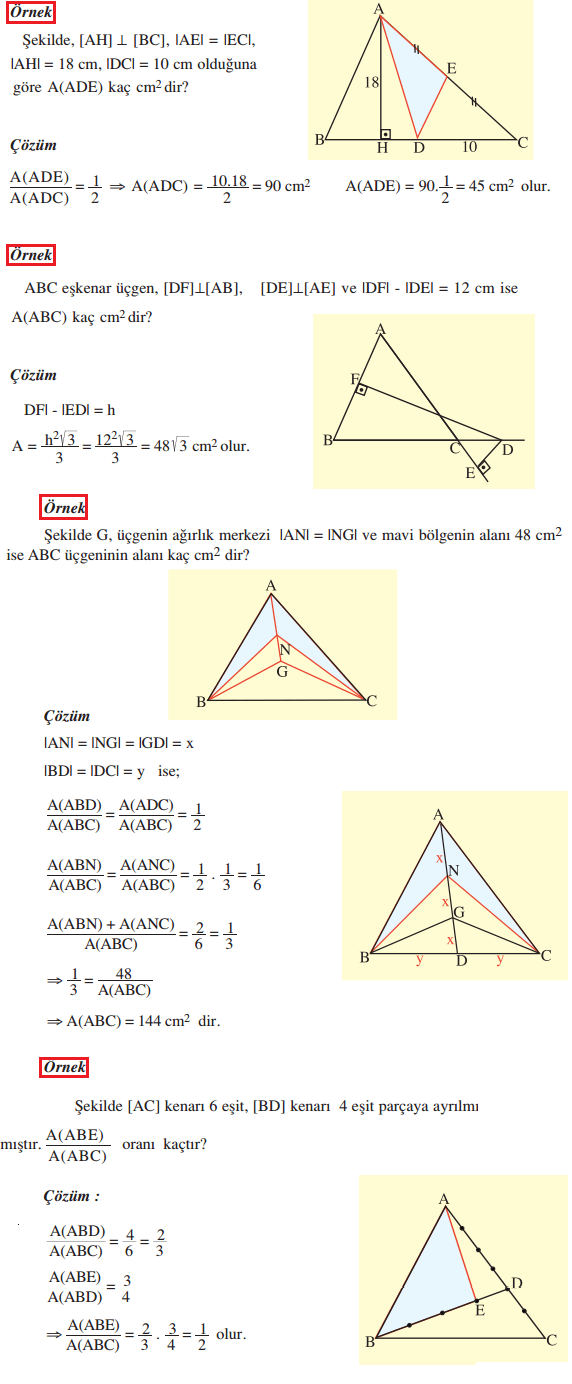



Ucgende Alan Formulleri Ucgenin Alan Formulu Bagintilari



Dik Ucgen Ozellikleri Nelerdir




Pdf Carbon Concentrations Of Tree Components Forest Floor And Understory In Young Pinus Sylvestris Stands In North Western Turkey



0 件のコメント:
コメントを投稿